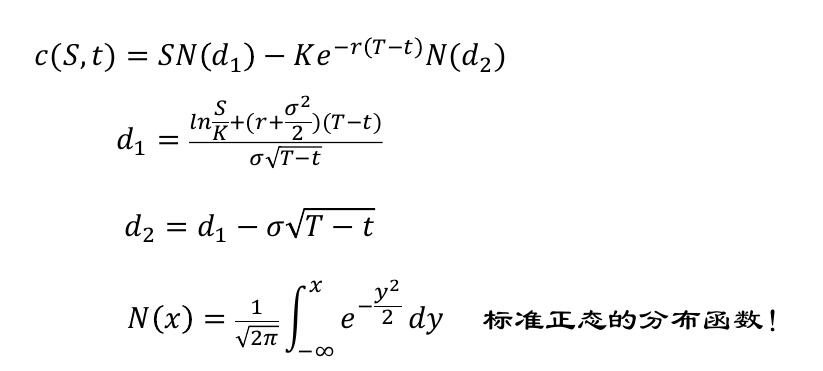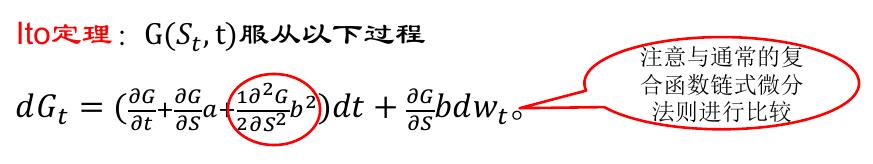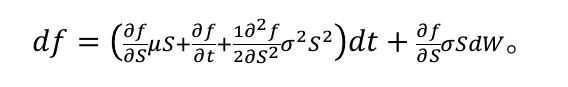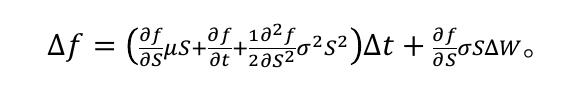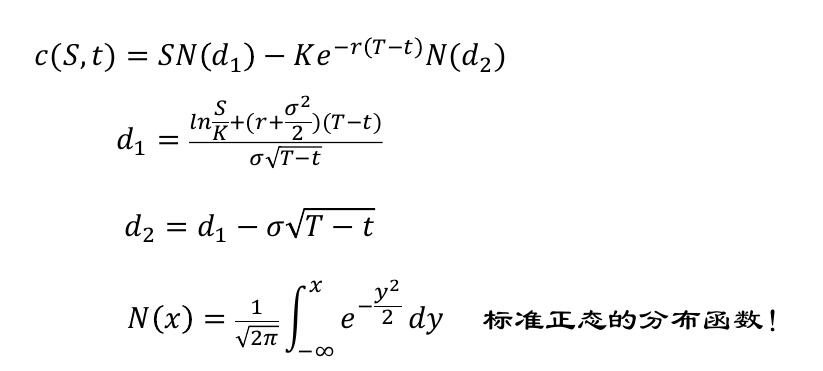1. 数理金融(六)
关于股票价格的连续时间 随机过程
1.1.1. 布朗运动
什么是布朗运动
一个随机过程w(t) 称为 标准布朗运动,如果满足以下性质:
- w(0)=0,w(t)关于时间连续
- 在给定的长度为Δt的时间区间上, w(t)的变化量Δw服从期望为0、方差为Δt的正态分布,即Δw=√Δtϕ,ϕ∼N(0,1) 。
- 在任意两个不互相重叠的时间区间上,变化量\Delta w是相互独立的。
- 第三个性质说明, w(t)服从马尔可夫过程,即w(t)在未来的概率分布只与当前值有关,而不依赖于在过去所遵循的特定路径。换句话说,该过程的当前值包含了对其未来做预测所需的全部信息。
利用matlab模拟[0,T]布朗运动
T=1; dt=1/1000; N=1001;
W=zeros(N,1);
for i=2:N
W(i)=W(i-1)+sqrt(dt)*randn;
end
plot([0:dt:T],W)
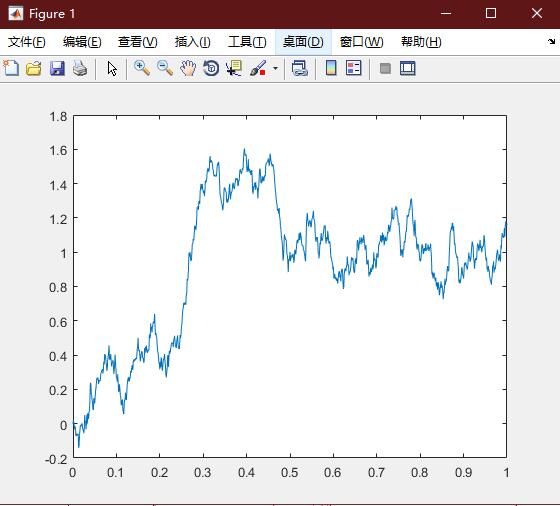
布朗运动的一些应用
一维布朗运动的走势和股票价格曲线的走势看着非常相似,这变引起人们利用它来描述股票价格走势的兴趣。
布朗运动 {w(t),t≥0} 的每一条轨道看起来是不光滑的,甚至是杂乱无章的,但它们是连续的。
值得注意的是布朗运动{w(t),t≥0} 的轨道是不可微的。
事实上,P(limΔt→0∣ΔtΔWt>x)=1
1.1.2. Ito过程与Ito积分
相关定义
我们定义xt为Ito过程,如果:
dxt=a(xt,t)dt+b(xt,t)dwt
dwt是标准布朗运动$W_t$在t时刻的瞬间改变量,dwt ~ N(0,dt).
a(xt,t)dt和b(xt,t)dt可以理解为xt 在t时刻的瞬间改变量的期望值和方差。𝑎称为过程xt的漂移率,𝑏称为xt 的扩散率。、

股票价格过程
标准布朗运动不是描述股价运动的最佳选择:因为在任意一个时间区间上改变量的期望都是0.
在衍生产品定价中,我们假设服从 Black-sholes模型
dSt=μStdt+σStdwt
μ,σ是常数
dSt是资产价格在无穷小的时间间隔内的变化量
dSt/St是这段时间内的收益率
所以 dSt/St=μdt+σdwt
这里称St是一个 几何布朗运动;μ 被称作资产阶级的期望收益率; σ 被称为资产阶级的波动率。
Ito定理
假定 G(St,t)是t和St 的二元函数,St 服从Ito过程
dSt=a(St,t)dt+b(St,t)dWt
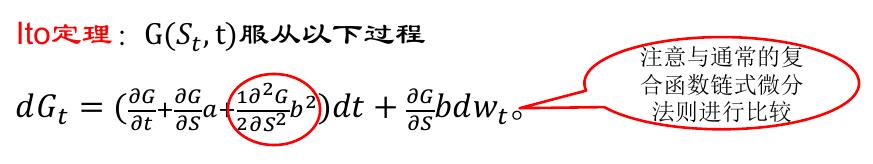
Ito定理的应用
用Ito定理计算 Ito积分


1.1.3. Black-schols方程的推导和应用
假设股票价格遵循几何布朗运动,即
dS=μSdt+σSdW
假定f为依赖于S的衍生产品价格,f(S,t),根据Ito定理
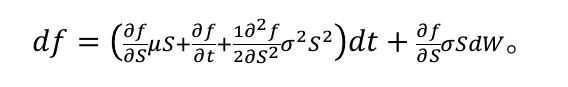
近似离散形式:
ΔS=μSΔt+σSΔdW
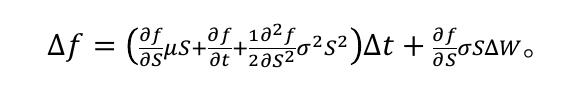

由于投资组合在长度为\Delta t的时间上市无风险的,根据无套利原理,无风险投资组合的收益率等于无风险收益率,所以有

- 欧式看涨期权的价格满足BC方程,其终值条件:f(S,T)=(S−K)+
- 欧式看跌期权的价格满足BC方程,其终值条件:f(S,T)=(K−S)+
注: 在BC方程中并未出现股票在真实世界里的期望回报率μ ,代替的是无风险收益率,因此BC得到的期权价格和μ无关

通过求解 BC方程,欧式看涨与看跌期权的价格如下: